2458 字
12 分钟
通过点坐标, 反求贝塞尔曲线对应的时间参数
2024-10-03
笔记
.NET
/
CSharp
/
算法

贝塞尔曲线在二维上的算法, 可以分解成两个相同的一维上的算法. 而任意阶的贝塞尔曲线都可以写作一个方程. 有方程, 就能尝试求解.

本文所有代码均已上传至 GitHub 仓库: SlimeNull/SolveBezierCurve

算法概述#

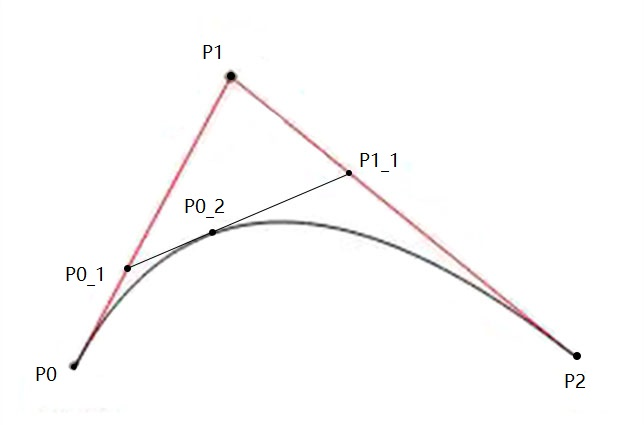
bezier2

以二阶贝塞尔曲线开始, 它有三个控制点, 构成了两个线段. 计算指定时间 t 上的点, 步骤如下:

  1. 在两个线段上, 取得进度为 t 的点, 得到两个点, 即一个线段
  2. 在一个线段上, 取得进度为 t 的点, 得到一个点, 即结果.

这里说的 “进度为 t 的点”, 则是对两点进行插值, t 为参数. 当 t 越接近 0 时, 结果越接近起始点. 当 t 越接近 1 时, 结果越接近结束点.

写成 C# 代码如下:

// 定义表示 Point 的结构体
public record struct Point(double X, double Y);

public class BezierUtilities
{
    // 对 double 进行插值的函数
    public static double Lerp(double a, double b, double t)
    {
        return a * (1 - t) + b * t;
    }

    // 对 Point 进行插值的函数
    public static Point Lerp(Point a, Point b, double t)
    {
        return new Point(Lerp(a.X, b.X, t), Lerp(a.Y, b.Y, t));
    }
}

同理, 三阶贝塞尔曲线由四个控制点, 也就是三个线段构成, 其计算过程如下:

  1. 在三个线段上, 取得进度为 t 的点, 得到三个点, 即两个线段
  2. 在两个线段上, 取得进度为 t 的点, 得到两个点, 即一个线段
  3. 在一个线段上, 取得进度为 t 的点, 得到一个点, 即结果.

可以看到, 不论多少阶的贝塞尔曲线, 其算法都是单调的

逻辑拆解#

通过前面的插值算法可以知道, 贝塞尔曲线不同维度上的计算结果互不影响, 也就是说, 我们完全可以将二维上的二阶贝塞尔曲线, 降维到一维. 这样, 原本由两个值构成的 “控制点”, 现在变成了纯数字.

二阶贝塞尔曲线#

那么接下来, 设一维二阶贝塞尔曲线三个控制点的值分别为 a, b, c , 时间参数为 t, 计算逻辑如下:

  1. 计算线段 a-b 之间的插值点 d=a×(1−t)+b×td = a \times (1 - t) + b \times t
    计算线段 b-c 之间的插值点 e=b×(1−t)+c×te = b \times (1 - t) + c \times t
  2. 计算线段 d-e 之间的插值点, 即最终的插值点: r=d×(1−t)+e×tr = d \times (1 - t) + e \times t

将它们展开, 最终的计算公式是:

r=(a×(1−t)+b×t)×(1−t)+(b×(1−t)+c×t)×tr = (a \times (1 - t) + b \times t) \times (1 - t) + (b \times (1 - t) + c \times t) \times t

即:

r=at2−2at+a−2bt2+2bt+ct2r = a t^2 - 2 a t + a - 2 b t^2 + 2 b t + c t^2

对于编程中的 “动画” 所使用的贝塞尔曲线, a 为 0, c 为 1, 此时公式是:

r=−2bt2+2bt+t2r = - 2 b t^2 + 2 b t + t^2

当 b 值确定时, 这就是一个简单的一元二次方程. 将其化为标准形式:

(−2b+1)t2+2bt−r=0(- 2b + 1) t^2 + 2 b t - r = 0

随便扔给 WolframAlpha 就能得出:

  • 当 b 为 0.5 时, 此时解为: t=rt = r
  • 当 b 不为 0.5 时, 解: r=b±b2−2br+r2b−1r = \frac{b \pm \sqrt{b^2 - 2br + r}}{2b - 1}

三阶贝塞尔曲线#

对于三阶贝塞尔曲线,

那么接下来, 设一维二阶贝塞尔曲线三个控制点的值分别为 a, b, c , 时间参数为 t, 计算逻辑如下:

  1. 计算线段 a-b 之间的插值点 e=a×(1−t)+b×te = a \times (1 - t) + b \times t
    计算线段 b-c 之间的插值点 f=b×(1−t)+c×tf = b \times (1 - t) + c \times t
    计算线段 c-d 之间的插值点 g=c×(1−t)+d×tg = c \times (1 - t) + d \times t
  2. 计算线段 e-f 之间的插值点 h=e×(1−t)+f×th = e \times (1 - t) + f \times t
    计算线段 f-g 之间的插值点 i=f×(1−t)+g×ti = f \times (1 - t) + g \times t
  3. 计算线段 h-i 之间的插值点, 即最终的插值点: r=h×(1−t)+i×tr = h \times (1 - t) + i \times t

将它们展开, 最终的计算公式是:

r=((a×(1−t)+b×t)×(1−t)+(b×(1−t)+c×t)×t)×(1−t)+((b×(1−t)+c×t)×(1−t)+(c×(1−t)+d×t)×t)×tr = ((a \times (1 - t) + b \times t) \times (1 - t) + (b \times (1 - t) + c \times t) \times t) \times (1 - t) + ((b \times (1 - t) + c \times t) \times (1 - t) + (c \times (1 - t) + d \times t) \times t) \times t

即:

r=−at3+3at2−3at+a+3bt3−6bt2+3bt−3ct3+3ct2+dt3r = -a t^3 + 3 a t^2 - 3 a t + a + 3 b t^3 - 6 b t^2 + 3 b t - 3 c t^3 + 3 c t^2 + d t^3

对于编程中的 “动画” 所使用的贝塞尔曲线, a 为 0, d 为 1, 此时公式是:

r=3bt3−6bt2+3bt−3ct3+3ct2+t3r = 3 b t^3 - 6 b t^2 + 3 b t - 3 c t^3 + 3 c t^2 + t^3

当 b 值确定时, 这就是一个简单的一元二次方程. 将其化为标准形式:

(3b−3c+1)t3+(−6b+3c)t2+3bt−r=0(3b - 3c + 1)t^3 + (-6b + 3c)t^2 + 3bt - r = 0

当然, 三次方程的求根公式就比二次方程的复杂多了, 在这就不写出来了. 在下一部分中给出的逻辑代码, 使用的是盛金法求三次方程.

选取合适的根#

对于贝塞尔曲线, t 的值应该总是大于等于 0, 小于等于 1 的. 所以在解方程之后, 不在此范围的根应该抛弃掉.

代码实现#

简单抽象一个 “点”:

public record struct Point(double X, double Y)
{
    public bool IsEmpty
    {
        [MethodImpl(MethodImplOptions.AggressiveInlining)]
        get => Is(0, 0);
    }

    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public bool Is(double x, double y) => X == x && Y == y;

    public static Point operator +(Point p1, Point p2)
    {
        return new Point(p1.X + p2.X, p1.Y + p2.Y);
    }

    public static Point operator -(Point p1, Point p2)
    {
        return new Point(p1.X - p2.X, p1.Y - p2.Y);
    }

    public static Point operator *(Point point, double factor)
    {
        return new Point(point.X * factor, point.Y * factor);
    }

    public static Point operator /(Point point, double factor)
    {
        return new Point(point.X / factor, point.Y / factor);
    }

    public static Point Lerp(Point a, Point b, double t)
    {
        return a * (1 - t) + b * t;
    }
}

一次方程, 二次方程, 三次方程的求解逻辑:

internal static class MathUtilities
{
    /// <summary>
    /// 解一元一次方程 (标准形式)
    /// </summary>
    /// <param name="a"></param>
    /// <param name="b"></param>
    /// <returns></returns>
    public static IEnumerable<double> SolveLinearFunction(double a, double b)
    {
        yield return -b / a;
    }

    /// <summary>
    /// 解一元二次方程 (标准形式)
    /// </summary>
    /// <param name="a">二次项系数</param>
    /// <param name="b">一次项系数</param>
    /// <param name="c">常数项</param>
    /// <returns></returns>
    public static IEnumerable<double> SolveQuadraticFunction(double a, double b, double c)
    {
        if (a == 0)
        {
            foreach (var root in SolveLinearFunction(b, c))
            {
                yield return root;
            }

            yield break;
        }

        var delta = b * b - 4 * a * c;
        if (delta < 0)
        {
            // 没有实数根
            yield break;
        }

        var x1 = (-b + Math.Sqrt(delta)) / (2 * a);
        yield return x1;

        if (delta == 0)
        {
            yield break;
        }

        var x2 = (-b - Math.Sqrt(delta)) / (2 * a);
        yield return x2;
    }

    /// <summary>
    /// 解一元三次方程 (标准形式)
    /// </summary>
    /// <param name="a">三次项系数</param>
    /// <param name="b">二次项系数</param>
    /// <param name="c">一次项系数</param>
    /// <param name="d">常数项</param>
    /// <returns></returns>
    public static IEnumerable<double> SolveCubicFunction(double a, double b, double c, double d)
    {
        if (a == 0)
        {
            foreach (var root in SolveQuadraticFunction(b, c, d))
            {
                yield return root;
            }

            yield break;
        }

        // 盛金公式法

        double bigA = b * b - 3 * a * c;
        double bigB = b * c - 9 * a * d;
        double bigC = c * c - 3 * b * d;

        double delta = bigB * bigB - 4 * bigA * bigC;

        if (bigA == bigB && bigA == 0)
        {
            // 三个相同的实数根
            yield return -c / b;
            yield break;
        }
        else if (delta > 0)
        {
            var bigY1 = bigA * b + 3 * a * ((-bigB + Math.Sqrt(delta)) / 2);
            var bigY2 = bigA * b + 3 * a * ((-bigB - Math.Sqrt(delta)) / 2);

            // 只有一个实数根, 剩下两个是虚的
            yield return (-b - (Math.Pow(bigY1, 1.0 / 3.0) + Math.Pow(bigY2, 1.0 / 3.0))) / (3 * a);
        }
        else if (delta == 0)
        {
            var bigK = bigB / bigA;

            yield return -b / a + bigK;

            // 两个相同的实数根
            yield return -bigK / 2;
        }
        else
        {
            var bigT = (2 * bigA * b - 3 * a * bigB) / (2 * Math.Pow(bigA, 3.0 / 2.0));
            var theta = Math.Acos(bigT);

            // 三个根
            yield return (-b - 2 * Math.Sqrt(bigA) * Math.Cos(theta / 3)) / (3 * a);
            yield return (-b + Math.Sqrt(bigA) * (Math.Cos(theta / 3) + Math.Sqrt(3) * Math.Sin(theta / 3))) / (3 * a);
            yield return (-b + Math.Sqrt(bigA) * (Math.Cos(theta / 3) - Math.Sqrt(3) * Math.Sin(theta / 3))) / (3 * a);
        }
    }
}

贝塞尔曲线抽象:

public class BezierCurve
{
    private readonly Point[] _points;

    public BezierCurve(IEnumerable<Point> points)
    {
        ArgumentNullException.ThrowIfNull(points);

        _points = points.ToArray();

        if (_points.Length < 1)
        {
            throw new ArgumentException("Point count can not be less than 1");
        }
    }

    private double SolveTimeForPoint(double controlPoint1, double controlPoint2, double point)
    {
        double a = -controlPoint1 + controlPoint2;
        double b = controlPoint1  - point;


        foreach (var root in MathUtilities.SolveLinearFunction(a, b))
        {
            if (root < 0 || root > 1)
            {
                continue;
            }

            return root;
        }

        return double.NaN;
    }

    private double SolveTimeForPoint(double controlPoint1, double controlPoint2, double controlPoint3, double point)
    {
        double a = controlPoint1 - 2 * controlPoint2 + controlPoint3;
        double b = -2 * controlPoint1 + 2 * controlPoint2;
        double c = controlPoint1 - point;

        foreach (var root in MathUtilities.SolveQuadraticFunction(a, b, c))
        {
            if (root < 0 || root > 1)
            {
                continue;
            }

            return root;
        }

        return double.NaN;
    }

    private double SolveTimeForPoint(double controlPoint1, double controlPoint2, double controlPoint3, double controlPoint4, double point)
    {
        double a = -controlPoint1 + 3 * controlPoint2 - 3 * controlPoint3 + controlPoint4;
        double b = 3 * controlPoint1 - 6 * controlPoint2 + 3 * controlPoint3;
        double c = -3 * controlPoint1 + 3 * controlPoint2;
        double d = controlPoint1 - point;

        foreach (var root in MathUtilities.SolveCubicFunction(a, b, c, d))
        {
            if (root < 0 || root > 1)
            {
                continue;
            }

            return root;
        }

        return double.NaN;
    }

    /// <summary>
    /// 传入进度 t 值, 求曲线上点坐标
    /// </summary>
    /// <param name="t"></param>
    /// <returns></returns>
    public Point Solve(double t)
    {
        Point[] buffer = new Point[_points.Length];
        _points.CopyTo(buffer, 0);

        int pointCount = _points.Length;
        while (pointCount > 1)
        {
            for (int i = 0; i < pointCount - 1; i++)
            {
                buffer[i] = Point.Lerp(buffer[i], buffer[i + 1], t);
            }

            pointCount--;
        }

        return buffer[0];
    }

    /// <summary>
    /// 根据曲线上某点的 X 值求解 t 参数
    /// </summary>
    /// <param name="pointX"></param>
    /// <returns></returns>
    /// <exception cref="NotSupportedException"></exception>
    public double SolveTimeForPointX(double pointX)
    {
        if (_points.Length == 2)
        {
            return SolveTimeForPoint(_points[0].X, _points[1].X, pointX);
        }
        else if (_points.Length == 3)
        {
            return SolveTimeForPoint(_points[0].X, _points[1].X, _points[2].X, pointX);
        }
        else if (_points.Length == 4)
        {
            return SolveTimeForPoint(_points[0].X, _points[1].X, _points[2].X, _points[3].X, pointX);
        }
        else
        {
            throw new NotSupportedException();
        }
    }

    /// <summary>
    /// 根据曲线上某点的 Y 值求解 t 参数
    /// </summary>
    /// <param name="pointY"></param>
    /// <returns></returns>
    /// <exception cref="NotSupportedException"></exception>
    public double SolveTimeForPointY(double pointY)
    {
        if (_points.Length == 2)
        {
            return SolveTimeForPoint(_points[0].Y, _points[1].Y, pointY);
        }
        else if (_points.Length == 3)
        {
            return SolveTimeForPoint(_points[0].Y, _points[1].Y, _points[2].Y, pointY);
        }
        else if (_points.Length == 4)
        {
            return SolveTimeForPoint(_points[0].Y, _points[1].Y, _points[2].Y, _points[3].Y, pointY);
        }
        else
        {
            throw new NotSupportedException();
        }
    }
}
通过点坐标, 反求贝塞尔曲线对应的时间参数
https://slimenull.com/posts/202410030450/
作者
SlimeNull
发布于
2024-10-03
许可协议
CC BY-NC-SA 4.0
如何优雅的在一个解决方案内使 C# 项目引用 C++ 库项目
在 WPF 中使用 ASP.NET Core 处理 HTTP 请求
© 2024 SlimeNull. All Rights Reserved. / RSS / Sitemap
Powered by Astro & Fuwari