关于向量:#

1. 向量的基#

在计算机科学中, 向量, Vector, 通常这么表示:

$$\left[ \begin{array}{cc} x\\ y \end{array} \right]$$

向量有两个 “基”, $\overline{i}$, 即 $\overrightarrow{1, 0}$, $\overline{j}$, 即 $\overrightarrow{0, 1}$

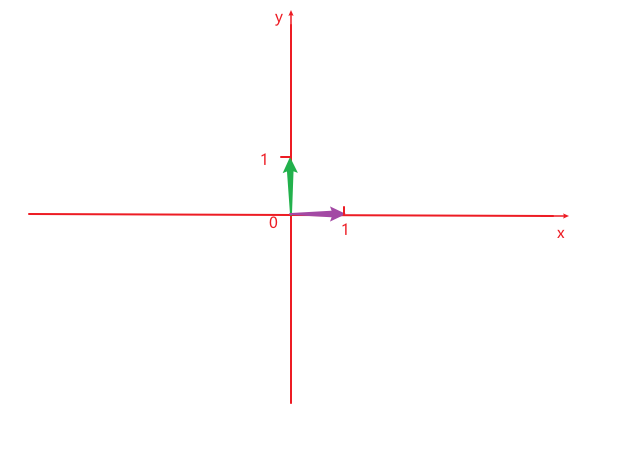
向量可以看作这些基乘以一组数的结果, 即: $\overline{v} = \overline{i} \times a + \overline{j} \times b$, 例如 $[1, 3]$, 就是:

$$\overline{i} \times 1 + \overline{j} \times 3 = [1, 0] \times 1 + [0, 1] \times 3 = [1, 0] + [0, 3] = [1, 3]$$

矩阵变换#

在 WPF 中, 一个矩阵(Matrix)有以下属性: M11, M12, M21, M22, OffsetX, OffsetY.

其中, M11, M12, M21, M22 表示缩放旋转矩阵:

它们的默认值是:

而进行矩阵变换, 也就是将源图形的每一个点, 与这个矩阵相乘, 最终得到另一些点, 构成一个新的图形.

而与默认的这个矩阵相乘, 形状不会有任何变化.

这个矩阵的 M11 和 M21 值, 可以理解为 $\overline i$, M12 和 M22 可以理解为 $\overline j$, 之前我们提到, 如果变化这两个基的值, 那么最终向量也会发生变化, 而当我们将刚刚旋转 90° 后的 $\overline i$ 和 $\overline j$ 拿出来直接代入, 也可以发现, 图形直接旋转了 90°.

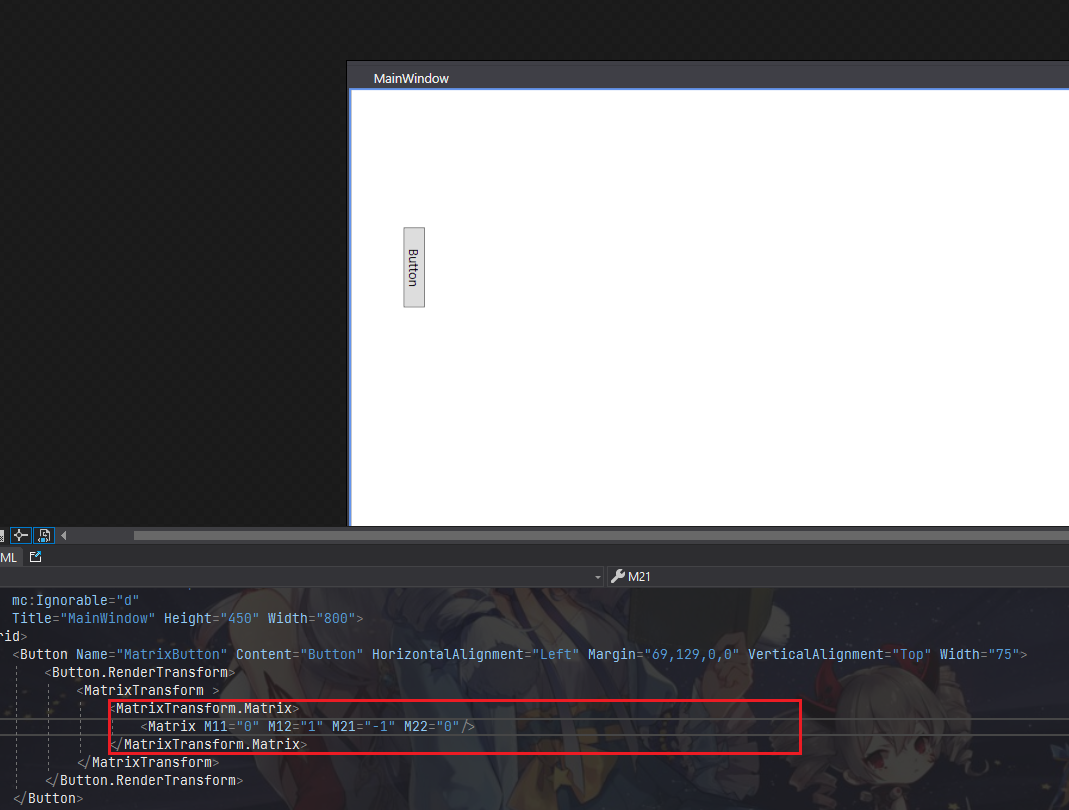
矩阵的基本原理就是矩阵的乘法, 但即便你不理解矩阵的乘法, 去改变 Matrix 中的两个基值, 形状也将跟随基值发生改变.

而 OffsetX 和 OffsetY, 这两个指定了这两个图形的平移, OffsetX 水平偏移量, OffsetY 垂直偏移量.

0. 参考内容:#

1. 哔哩哔哩 3Blue1Brown 线性代数
2. 理解矩阵乘法 - 阮一峰的网络日志
3. 矩阵乘法 - endl